5.4 KiB
前言
用于解决动态连通性问题,能动态连接两个点,并且判断两个点是否连通。
| 方法 | 描述 |
|---|---|
| UF(int N) | 构造一个大小为 N 的并查集 |
| void union(int p, int q) | 连接 p 和 q 节点 |
| int find(int p) | 查找 p 所在的连通分量编号 |
| boolean connected(int p, int q) | 判断 p 和 q 节点是否连通 |
public abstract class UF {
protected int[] id;
public UF(int N) {
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public abstract int find(int p);
public abstract void union(int p, int q);
}
Quick Find
可以快速进行 find 操作,也就是可以快速判断两个节点是否连通。
需要保证同一连通分量的所有节点的 id 值相等,就可以通过判断两个节点的 id 值是否相等从而判断其连通性。
但是 union 操作代价却很高,需要将其中一个连通分量中的所有节点 id 值都修改为另一个节点的 id 值。
public class QuickFindUF extends UF {
public QuickFindUF(int N) {
super(N);
}
@Override
public int find(int p) {
return id[p];
}
@Override
public void union(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID) {
return;
}
for (int i = 0; i < id.length; i++) {
if (id[i] == pID) {
id[i] = qID;
}
}
}
}
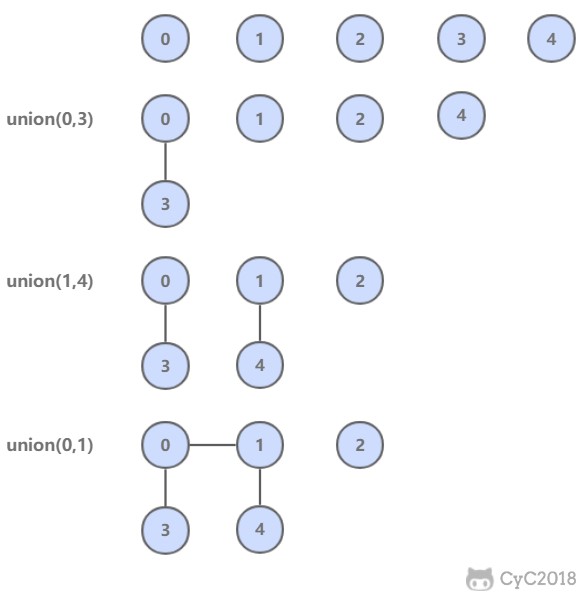
Quick Union
可以快速进行 union 操作,只需要修改一个节点的 id 值即可。
但是 find 操作开销很大,因为同一个连通分量的节点 id 值不同,id 值只是用来指向另一个节点。因此需要一直向上查找操作,直到找到最上层的节点。
public class QuickUnionUF extends UF {
public QuickUnionUF(int N) {
super(N);
}
@Override
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
@Override
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot != qRoot) {
id[pRoot] = qRoot;
}
}
}
这种方法可以快速进行 union 操作,但是 find 操作和树高成正比,最坏的情况下树的高度为节点的数目。
加权 Quick Union
为了解决 quick-union 的树通常会很高的问题,加权 quick-union 在 union 操作时会让较小的树连接较大的树上面。
理论研究证明,加权 quick-union 算法构造的树深度最多不超过 logN。
public class WeightedQuickUnionUF extends UF {
// 保存节点的数量信息
private int[] sz;
public WeightedQuickUnionUF(int N) {
super(N);
this.sz = new int[N];
for (int i = 0; i < N; i++) {
this.sz[i] = 1;
}
}
@Override
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
@Override
public void union(int p, int q) {
int i = find(p);
int j = find(q);
if (i == j) return;
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
}
}
路径压缩的加权 Quick Union
在检查节点的同时将它们直接链接到根节点,只需要在 find 中添加一个循环即可。
比较
| 算法 | union | find |
|---|---|---|
| Quick Find | N | 1 |
| Quick Union | 树高 | 树高 |
| 加权 Quick Union | logN | logN |
| 路径压缩的加权 Quick Union | 非常接近 1 | 非常接近 1 |
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。