12 KiB
3. 数组中重复的数字
题目描述
在一个长度为 n 的数组里的所有数字都在 0 到 n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字是重复的,也不知道每个数字重复几次。请找出数组中任意一个重复的数字。
Input:
{2, 3, 1, 0, 2, 5}
Output:
2
解题思路
要求时间复杂度 O(N),空间复杂度 O(1)。因此不能使用排序的方法,也不能使用额外的标记数组。
对于这种数组元素在 [0, n-1] 范围内的问题,可以将值为 i 的元素调整到第 i 个位置上进行求解。
以 (2, 3, 1, 0, 2, 5) 为例,遍历到位置 4 时,该位置上的数为 2,但是第 2 个位置上已经有一个 2 的值了,因此可以知道 2 重复:
public boolean duplicate(int[] nums, int length, int[] duplication) {
if (nums == null || length <= 0)
return false;
for (int i = 0; i < length; i++) {
while (nums[i] != i) {
if (nums[i] == nums[nums[i]]) {
duplication[0] = nums[i];
return true;
}
swap(nums, i, nums[i]);
}
}
return false;
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
4. 二维数组中的查找
题目描述
给定一个二维数组,其每一行从左到右递增排序,从上到下也是递增排序。给定一个数,判断这个数是否在该二维数组中。
Consider the following matrix:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
Given target = 5, return true.
Given target = 20, return false.
解题思路
要求时间复杂度 O(M + N),空间复杂度 O(1)。其中 M 为行数,N 为 列数。
该二维数组中的一个数,小于它的数一定在其左边,大于它的数一定在其下边。因此,从右上角开始查找,就可以根据 target 和当前元素的大小关系来缩小查找区间,当前元素的查找区间为左下角的所有元素。
public boolean Find(int target, int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return false;
int rows = matrix.length, cols = matrix[0].length;
int r = 0, c = cols - 1; // 从右上角开始
while (r <= rows - 1 && c >= 0) {
if (target == matrix[r][c])
return true;
else if (target > matrix[r][c])
r++;
else
c--;
}
return false;
}
5. 替换空格
题目描述
将一个字符串中的空格替换成 "%20"。
Input:
"A B"
Output:
"A%20B"
解题思路
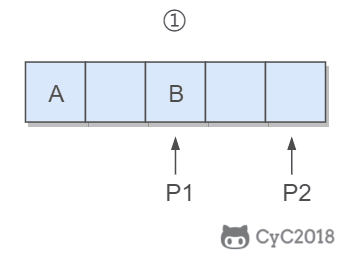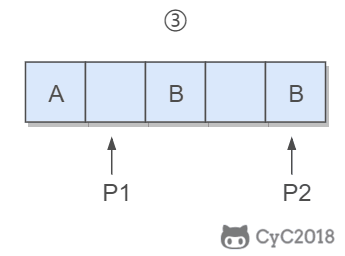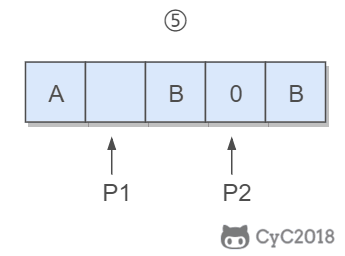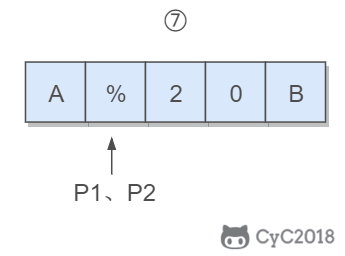
在字符串尾部填充任意字符,使得字符串的长度等于替换之后的长度。因为一个空格要替换成三个字符(%20),因此当遍历到一个空格时,需要在尾部填充两个任意字符。
令 P1 指向字符串原来的末尾位置,P2 指向字符串现在的末尾位置。P1 和 P2 从后向前遍历,当 P1 遍历到一个空格时,就需要令 P2 指向的位置依次填充 02%(注意是逆序的),否则就填充上 P1 指向字符的值。
从后向前遍是为了在改变 P2 所指向的内容时,不会影响到 P1 遍历原来字符串的内容。
public String replaceSpace(StringBuffer str) {
int P1 = str.length() - 1;
for (int i = 0; i <= P1; i++)
if (str.charAt(i) == ' ')
str.append(" ");
int P2 = str.length() - 1;
while (P1 >= 0 && P2 > P1) {
char c = str.charAt(P1--);
if (c == ' ') {
str.setCharAt(P2--, '0');
str.setCharAt(P2--, '2');
str.setCharAt(P2--, '%');
} else {
str.setCharAt(P2--, c);
}
}
return str.toString();
}
6. 从尾到头打印链表
题目描述
从尾到头反过来打印出每个结点的值。
解题思路
使用递归
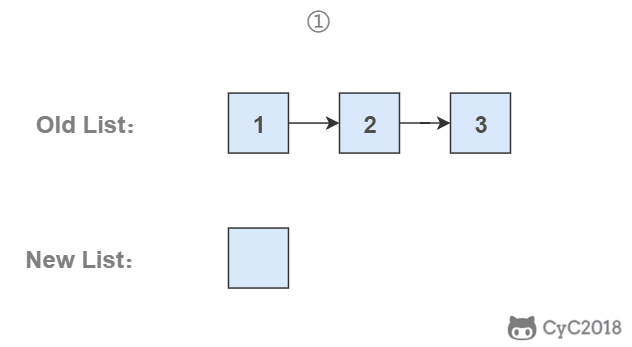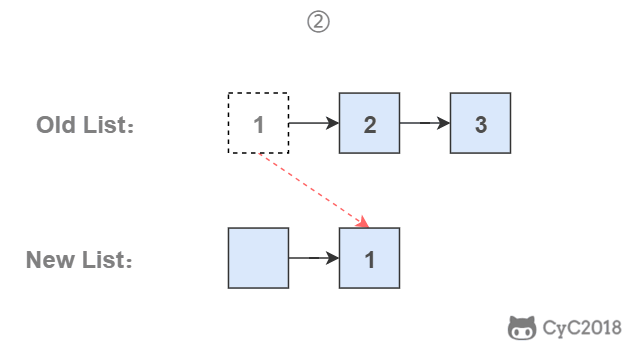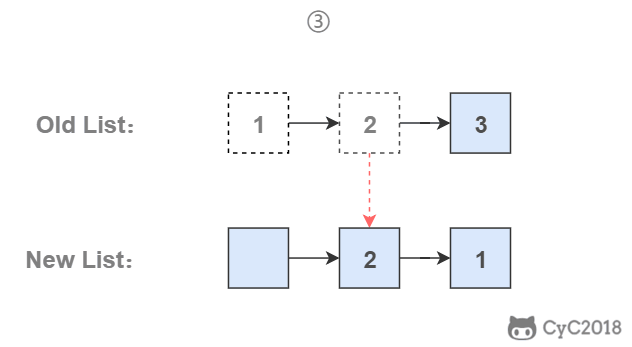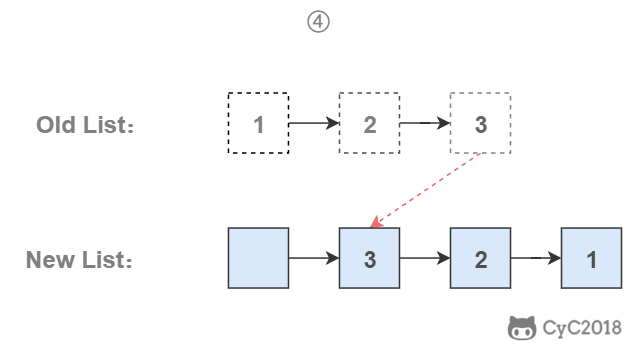
要逆序打印链表 1->2->3(3,2,1),可以先逆序打印链表 2->3(3,2),最后再打印第一个节点 1。而链表 2->3 可以看成一个新的链表,要逆序打印该链表可以继续使用求解函数,也就是在求解函数中调用自己,这就是递归函数。
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> ret = new ArrayList<>();
if (listNode != null) {
ret.addAll(printListFromTailToHead(listNode.next));
ret.add(listNode.val);
}
return ret;
}
使用头插法
使用头插法可以得到一个逆序的链表。
头结点和第一个节点的区别:
- 头结点是在头插法中使用的一个额外节点,这个节点不存储值;
- 第一个节点就是链表的第一个真正存储值的节点。
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
// 头插法构建逆序链表
ListNode head = new ListNode(-1);
while (listNode != null) {
ListNode memo = listNode.next;
listNode.next = head.next;
head.next = listNode;
listNode = memo;
}
// 构建 ArrayList
ArrayList<Integer> ret = new ArrayList<>();
head = head.next;
while (head != null) {
ret.add(head.val);
head = head.next;
}
return ret;
}
使用栈
栈具有后进先出的特点,在遍历链表时将值按顺序放入栈中,最后出栈的顺序即为逆序。
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
Stack<Integer> stack = new Stack<>();
while (listNode != null) {
stack.add(listNode.val);
listNode = listNode.next;
}
ArrayList<Integer> ret = new ArrayList<>();
while (!stack.isEmpty())
ret.add(stack.pop());
return ret;
}
7. 重建二叉树
题目描述
根据二叉树的前序遍历和中序遍历的结果,重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
解题思路
前序遍历的第一个值为根节点的值,使用这个值将中序遍历结果分成两部分,左部分为树的左子树中序遍历结果,右部分为树的右子树中序遍历的结果。
// 缓存中序遍历数组每个值对应的索引
private Map<Integer, Integer> indexForInOrders = new HashMap<>();
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
for (int i = 0; i < in.length; i++)
indexForInOrders.put(in[i], i);
return reConstructBinaryTree(pre, 0, pre.length - 1, 0);
}
private TreeNode reConstructBinaryTree(int[] pre, int preL, int preR, int inL) {
if (preL > preR)
return null;
TreeNode root = new TreeNode(pre[preL]);
int inIndex = indexForInOrders.get(root.val);
int leftTreeSize = inIndex - inL;
root.left = reConstructBinaryTree(pre, preL + 1, preL + leftTreeSize, inL);
root.right = reConstructBinaryTree(pre, preL + leftTreeSize + 1, preR, inL + leftTreeSize + 1);
return root;
}
8. 二叉树的下一个结点
题目描述
给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
public class TreeLinkNode {
int val;
TreeLinkNode left = null;
TreeLinkNode right = null;
TreeLinkNode next = null;
TreeLinkNode(int val) {
this.val = val;
}
}
解题思路
① 如果一个节点的右子树不为空,那么该节点的下一个节点是右子树的最左节点;
② 否则,向上找第一个左链接指向的树包含该节点的祖先节点。
public TreeLinkNode GetNext(TreeLinkNode pNode) {
if (pNode.right != null) {
TreeLinkNode node = pNode.right;
while (node.left != null)
node = node.left;
return node;
} else {
while (pNode.next != null) {
TreeLinkNode parent = pNode.next;
if (parent.left == pNode)
return parent;
pNode = pNode.next;
}
}
return null;
}
9. 用两个栈实现队列
题目描述
用两个栈来实现一个队列,完成队列的 Push 和 Pop 操作。
解题思路
in 栈用来处理入栈(push)操作,out 栈用来处理出栈(pop)操作。一个元素进入 in 栈之后,出栈的顺序被反转。当元素要出栈时,需要先进入 out 栈,此时元素出栈顺序再一次被反转,因此出栈顺序就和最开始入栈顺序是相同的,先进入的元素先退出,这就是队列的顺序。
Stack<Integer> in = new Stack<Integer>();
Stack<Integer> out = new Stack<Integer>();
public void push(int node) {
in.push(node);
}
public int pop() throws Exception {
if (out.isEmpty())
while (!in.isEmpty())
out.push(in.pop());
if (out.isEmpty())
throw new Exception("queue is empty");
return out.pop();
}
更多精彩内容将发布在公众号 CyC2018,公众号提供了该项目的离线阅读版本,后台回复"下载" 即可领取。也提供了一份技术面试复习思维导图,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复"资料" 即可领取。。我基本是按照这个思维导图来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据思维导图上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。