diff --git a/docs/notes/剑指 Offer 题解 - 10~19.md b/docs/notes/剑指 Offer 题解 - 10~19.md
index e7d1d732..e4e4ec26 100644
--- a/docs/notes/剑指 Offer 题解 - 10~19.md
+++ b/docs/notes/剑指 Offer 题解 - 10~19.md
@@ -232,16 +232,20 @@ public int JumpFloorII(int target) {
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
-例如数组 {3, 4, 5, 1, 2} 为 {1, 2, 3, 4, 5} 的一个旋转,该数组的最小值为 1。
+
## 解题思路
-在一个有序数组中查找一个元素可以用二分查找,二分查找也称为折半查找,每次都能将查找区间减半,这种折半特性的算法时间复杂度都为 O(logN)。
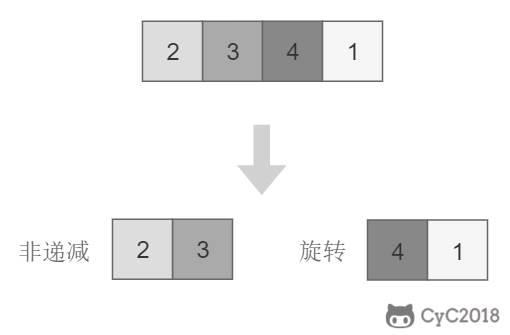
+将旋转数组对半分可以得到一个包含最小元素的新旋转数组,以及一个非递减排序的数组。新的旋转数组的数组元素是原数组的一半,从而将问题规模减少了一半,这种折半性质的算法的时间复杂度为 O(logN)(为了方便,这里将 log2N 写为 logN)。
-本题可以修改二分查找算法进行求解:
+
-- 当 nums[m] <= nums[h] 的情况下,说明解在 [l, m] 之间,此时令 h = m;
-- 否则解在 [m + 1, h] 之间,令 l = m + 1。
+此时问题的关键在于确定对半分得到的两个数组哪一个是旋转数组,哪一个是非递减数组。我们很容易知道非递减数组的第一个元素一定小于等于最后一个元素。
+
+通过修改二分查找算法进行求解(l 代表 low,m 代表 mid,h 代表 high):
+
+- 当 nums[m] <= nums[h] 时,表示 [m, h] 区间内的数组是非递减数组,[l, m] 区间内的数组是旋转数组,此时令 h = m;
+- 否则 [m + 1, h] 区间内的数组是旋转数组,令 l = m + 1。
```java
public int minNumberInRotateArray(int[] nums) {
@@ -259,7 +263,7 @@ public int minNumberInRotateArray(int[] nums) {
}
```
-如果数组元素允许重复的话,那么就会出现一个特殊的情况:nums[l] == nums[m] == nums[h],那么此时无法确定解在哪个区间,需要切换到顺序查找。例如对于数组 {1,1,1,0,1},l、m 和 h 指向的数都为 1,此时无法知道最小数字 0 在哪个区间。
+如果数组元素允许重复,会出现一个特殊的情况:nums[l] == nums[m] == nums[h],此时无法确定解在哪个区间,需要切换到顺序查找。例如对于数组 {1,1,1,0,1},l、m 和 h 指向的数都为 1,此时无法知道最小数字 0 在哪个区间。
```java
public int minNumberInRotateArray(int[] nums) {
diff --git a/docs/pics/0038204c-4b8a-42a5-921d-080f6674f989.png b/docs/pics/0038204c-4b8a-42a5-921d-080f6674f989.png
new file mode 100644
index 00000000..31a2d8d2
Binary files /dev/null and b/docs/pics/0038204c-4b8a-42a5-921d-080f6674f989.png differ
diff --git a/docs/pics/424f34ab-a9fd-49a6-9969-d76b42251365.png b/docs/pics/424f34ab-a9fd-49a6-9969-d76b42251365.png
new file mode 100644
index 00000000..d5c1a58d
Binary files /dev/null and b/docs/pics/424f34ab-a9fd-49a6-9969-d76b42251365.png differ
diff --git a/notes/pics/0038204c-4b8a-42a5-921d-080f6674f989.png b/notes/pics/0038204c-4b8a-42a5-921d-080f6674f989.png
new file mode 100644
index 00000000..31a2d8d2
Binary files /dev/null and b/notes/pics/0038204c-4b8a-42a5-921d-080f6674f989.png differ
diff --git a/notes/pics/424f34ab-a9fd-49a6-9969-d76b42251365.png b/notes/pics/424f34ab-a9fd-49a6-9969-d76b42251365.png
new file mode 100644
index 00000000..d5c1a58d
Binary files /dev/null and b/notes/pics/424f34ab-a9fd-49a6-9969-d76b42251365.png differ
diff --git a/notes/剑指 Offer 题解 - 10~19.md b/notes/剑指 Offer 题解 - 10~19.md
index c1ec071a..6902dddd 100644
--- a/notes/剑指 Offer 题解 - 10~19.md
+++ b/notes/剑指 Offer 题解 - 10~19.md
@@ -232,16 +232,20 @@ public int JumpFloorII(int target) {
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
-例如数组 {3, 4, 5, 1, 2} 为 {1, 2, 3, 4, 5} 的一个旋转,该数组的最小值为 1。
+
## 解题思路
-在一个有序数组中查找一个元素可以用二分查找,二分查找也称为折半查找,每次都能将查找区间减半,这种折半特性的算法时间复杂度都为 O(logN)。
+将旋转数组对半分可以得到一个包含最小元素的新旋转数组,以及一个非递减排序的数组。新的旋转数组的数组元素是原数组的一半,从而将问题规模减少了一半,这种折半性质的算法的时间复杂度为 O(logN)(为了方便,这里将 log2N 写为 logN)。
-本题可以修改二分查找算法进行求解:
+
-- 当 nums[m] <= nums[h] 的情况下,说明解在 [l, m] 之间,此时令 h = m;
-- 否则解在 [m + 1, h] 之间,令 l = m + 1。
+此时问题的关键在于确定对半分得到的两个数组哪一个是旋转数组,哪一个是非递减数组。我们很容易知道非递减数组的第一个元素一定小于等于最后一个元素。
+
+通过修改二分查找算法进行求解(l 代表 low,m 代表 mid,h 代表 high):
+
+- 当 nums[m] <= nums[h] 时,表示 [m, h] 区间内的数组是非递减数组,[l, m] 区间内的数组是旋转数组,此时令 h = m;
+- 否则 [m + 1, h] 区间内的数组是旋转数组,令 l = m + 1。
```java
public int minNumberInRotateArray(int[] nums) {
@@ -259,7 +263,7 @@ public int minNumberInRotateArray(int[] nums) {
}
```
-如果数组元素允许重复的话,那么就会出现一个特殊的情况:nums[l] == nums[m] == nums[h],那么此时无法确定解在哪个区间,需要切换到顺序查找。例如对于数组 {1,1,1,0,1},l、m 和 h 指向的数都为 1,此时无法知道最小数字 0 在哪个区间。
+如果数组元素允许重复,会出现一个特殊的情况:nums[l] == nums[m] == nums[h],此时无法确定解在哪个区间,需要切换到顺序查找。例如对于数组 {1,1,1,0,1},l、m 和 h 指向的数都为 1,此时无法知道最小数字 0 在哪个区间。
```java
public int minNumberInRotateArray(int[] nums) {